ООО "ЛАМЕТ"

Советские стандарты и соответствующая практика предусматривали два определения расходимости пучка.

 По интенсивности: плоский угол при вершине конуса вращения вокруг оптической оси, средняя сила излучения (энергии или мощности) на образующих которого составляет заданный уровень от максимальной силы излучения в данном пучке.

По энергии: плоский угол при вершине конуса вращения вокруг оптической оси, в пределах которого распространяется заданная доля излучения (энергии или мощности) от полного излучения пучка.

Оптической осью при этом считалась линия, проходящая через энергетический центр (центр тяжести) пучка в дальней зоне, т.е. на бесконечном удалении от лазера. Об эллиптичности пучков вопрос ставился, как правило, только как о временном недостатке, подлежащим устранению в ходе дальнейших работ.

В практическом применении того или иного из двух указанных критериев, а также того или иного «заданного уровня» наблюдался разнобой, обусловленный попытками ответить на два вопроса: - какой параметр и по какому уровню лучше отражает назначение лазера? - какой параметр и по какому уровню может быть проще и надежнее измерен? Только естественное желание, чтобы параметр был еще и наиболее репрезентативным для проведения сопоставительного анализа с другими лазерами, в том числе с зарубежными, несколько сужало выбор. В результате, как правило, использовались 4 варианта: - 2 уровня по интенсивности 0,5 или 1/е2 =0,135; - 2 уровня по энергии 0,5 или (1-1/е2)=0,865.

В настоящее время в результате вступления в ВТО, происходит присоединение России к международным стандартам, в том числе и в области измерения лазерных параметров. В отличие от советской «свободы выбора» стандарт ISO 11146 устанавливает одно-единственное определение расходимости как углового размера, определенного на основе вторых моментов (двух дисперсий и одного смешанного момента) распределения силы изучения (энергии или мощности) в пучке. В первых редакциях этого стандарта было, правда, примечание, что он не распространяется на лазеры с неустойчивыми резонаторами и, вообще, на пучки с резко ограничивающей апертурой. Однако в последних редакциях это примечание исчезло, что наводит на размышления.

Разумеется, для Гауссовых пучков данное определение никаких возражений не вызывает, тем более что для них данный угол равен углу по интенсивности на уровне 1/е2 =0,135 и углу по энергии на уровне (1-1/е2)=0,865. Однако в случаях, когда распределение в пучке сильно отличается от Гауссова, слепое следование указанному стандарту может оказаться нецелесообразным (см. примеры ниже).

Измеритель СИЭПХ-2 при измерениях автоматически измеряет и отображает значения диаметра пучка и расходимости по 25-ти критериям (см. ниже). Выбор за исследователем.

 Для понимания сути проблемы при измерении расходимости рассмотрим 8 вариантов волнового фронта на выходной апертуре лазера и 8 соответствующих распределений излучения в дальней зоне, формирующихся в результате свертки отдельных составляющих расходимости. Они разбиты на 2 группы: 1)пучки с резко ограничивающей апертурой и 2)Гауссовы пучки. У пучков первой группы интенсивность выходящего излучения на краю пучка резко падает до нуля, благодаря чему наблюдается относительно сильная дифракция. У Гауссовых пучков, конечно, тоже есть ограничивающая апертура, но ее край проходит там, где интенсивность выходящего излучения пренебрежимо мала, а диаметр отсчитывается там, где интенсивность излучения составляет 0,135 от максимального значения. Все варианты схематически отображены на рисунке.

Дадим краткий комментарий к приведенным вариантам : 1. Расходимость пучка идеального излучателя с плоским фронтом определяется только дифракцией на выходной апертуре. Расчет может быть проведен для выходной апертуры любой конфигурации. Для круглой апертуры с диаметром D эта (дифракционная ) расходимость обычно оценивается угловым размером диаметра первого темного кольца на картине Эйри, в пределах которого распространяется 0,84 полной энергии или мощности). Эта составляющая присутствует всегда. 2.При сферическом волновом фронте с радиусом R (неважно сходящемся или расходящемся) на выходной апертуре, основную роль играет геометрическая составляющая расходимости, определяемая соотношением D/R . Эта составляющая, в принципе, сравнительно легко устраняется установкой в пучке в нужном месте подходящей линзы. 3.Если волновой фронт, оставаясь в среднем плоским, в более мелком масштабе имеет неровности, обусловленные как наличием многих мод так и неоднородностями активной среды, расходимость пучка значительно превышает дифракционную и называется физической. Эта составляющая расходимости является самой важной как для разработчиков, так и для потребителей. Она определяет так называемую фокусируемость пучка. В отличие от геометрической она уменьшается непросто и за ее уменьшение идет тяжелая и изнурительная борьба. 4.Наиболее общий случай пучка с резко ограничивающей апертурой, когда присутствуют все составляющие расходимости. 5.Гауссов пучок диаметром D с плоским фронтом, распространяясь в пространстве, всегда сохраняет Гауссову форму (если не учитывать влияние атмосферы). Дифракционная расходимость такого пучка несколько превышает отношение длины волны к диаметру пучка. В пределах этого угла (почти в два раза меньшего, чем у излучателя с резкой апертурой) распространяется 0,865 полного излучения (энергии или мощности). 6. Сферический фронт также не оказывает влияния на форму распределения. Пучок везде остается Гауссовым, но его угловое уширение из-за геометрической составляющей расходимости определяется соотношением D/R . 7. Физическая расходимость обусловленная как наличием многих мод так и неоднородностями активной среды, разумеется, имеет в общем случае не Гауссову форму, и, как указывалось ранее определяет фокусируемость пучка. 8. Полная расходимость включает все составляющие. Ее форма будет значительно отличаться от Гауссовой только при большой физической расходимости. С точки зрения проведения практических измерений наиболее эффективным методом измерения расходимости является метод фокального пятна. При этом используется то обстоятельство, что линейные размеры в фокусе безаберрационной линзы строго пропорциональны угловым размерам в дальней зоне. В частности это относится к диаметру d и углу расходимости . Коэффициентом пропорциональности является фокусное расстояние линзы F . Таким образом, угол расходимости равен d/ F. Практические аспекты применения метода фокального пятна обсудим с использованием рисунка (все углы для наглядности утрированы).

Бросается в глаза, что в зависимости от положения линзы в расходящемся пучке фокусировка пучка осуществляется по-разному. При близком расположении линзы к излучающей апертуре лазера (зеленый вариант) перетяжка пучка расположена далеко за фокусом линзы и имеет большой поперечный размер. При более дальнем расположении линзы перетяжка сильно уменьшается в размере и приближается к фокусу линзы.

Возникает вопрос: есть ли какие – либо инварианты, не зависящие от положения линзы? Есть; и их - два: 1) распределение интенсивности в фокусе линзы не зависит от ее положения; соответственно идентичными сохраняются значения диаметра d пятна и расходимости d/ F по любому критерию и по любому уровню; 2) произведение диаметра перетяжки на угол расходимости сфокусированного пучка , являющееся параметром качества пучка ВРР (Beam Parameter Product).

Если первый инвариант (полная расходимость) определяется непосредственно в ходе одного эксперимента, то для определения второго требуется дополнительная работа. В частности необходимо уточнить положение перетяжки и значение ее диаметра, а также определить угол расходимости сфокусированного пучка. Кроме того, если расходимость по п.1) может определяться по любому критерию, то для диаметра перетяжки, и для угла расходимости, используемых при определении параметра ВРР согласно п.2), в общем случае в качестве критерия пригоден только второй момент.

Это объясняется изменением формы распределения интенсивности от перетяжки до зоны Рэлея и, следовательно, зависимостью коэффициентов гиперболической кривой от выбранного критерия и уровня. (Исключением является только случай сохранения Гауссова распределения вдоль всего пучка).

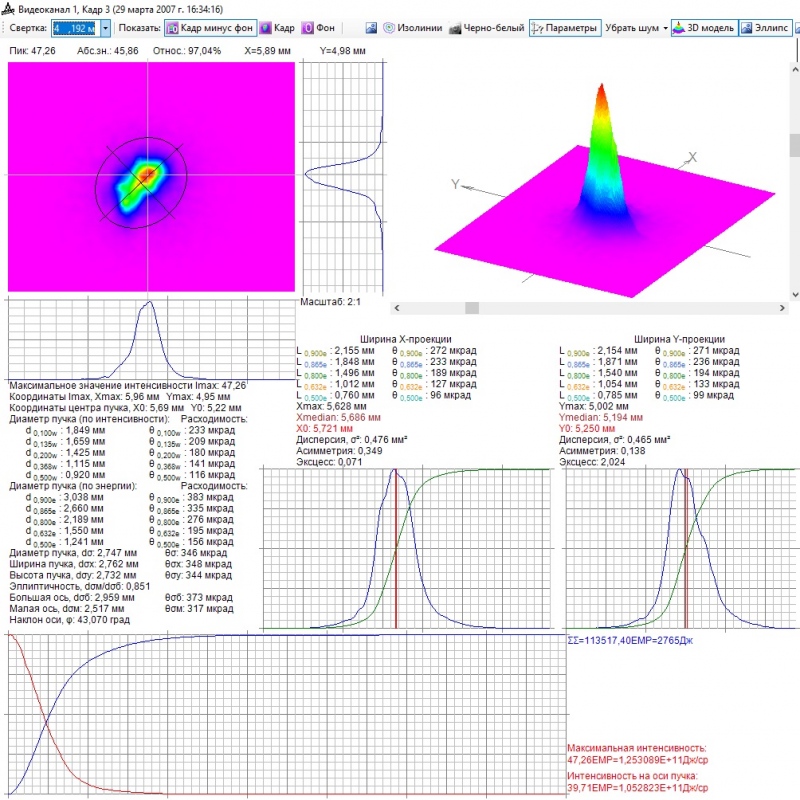
В заключение приведем два протокола измерения диаметра пучка и расходимости, сформированные программой измерителя СИЭПХ-2 на основе обработки двух различных распределений в фокальном пятне.

Распределение в первом протоколе имеет почти Гауссову форму. Об этом свидетельствуют близкие значения расходимости, определенные по различным критериям:
- по интенсивности по уровню 0,135 ……210 мкрад;
- по энергии по уровню 0,865……………..216 мкрад;
- по второму моменту………………………226 мкрад.
Наблюдается небольшая эллиптичность, но две кривые в нижней части протокола являются почти зеркальным отражением друг друга (красная кривая – падение интенсивности в зависимости от угла, отсчитываемого от оптической оси; синяя кривая – нарастание доли мощности в пределах конуса вращения вокруг оптической оси от половины угла при вершине) и пересекаются практически точно на уровне 0,5.

Форма распределения во втором протоколе резко отличается от первого. Центральное пятно окружено сравнительно слабым, но широким ореолом. Контрольные значения, определенные по различным критериям резко расходятся и составляют:
- по интенсивности по уровню 0,135 ……175 мкрад;
- по энергии по уровню 0,865………………590 мкрад;
- по второму моменту……………………….540 мкрад.
Две кривые в нижней части протокола также сильно отличаются; нарастание синей (интегральной) кривой значительно отстает от падения красной. В связи с этим целесообразность определения расходимости по второму моменту и в данном случае вызывает сомнения. В верхней правой части протокола вокруг центрального интенсивного пятна проведен эллипс (в данном случае почти круг), обозначающий размеры фокального пятна строго в соответствии с алгоритмом определения вторых моментов. Очевидно, что в пределах этого эллипса основную часть площади занимает кольцевая область, где интенсивность излучения очень мала по сравнению с центральной областью. Поэтому формально правильное (в соответствии со стандартом ISO 11146 ) определение угла расходимости, в данном случае явно неудобно и для разработчика, и для потребителя. На наш взгляд целесообразно сохранить возможность использования и других критериев определения угла расходимости. В данном случае удобно воспользоваться углом, определенным по интенсивности по уровню 0,135 , составляющим 175 мкрад. Тем более, что по случайному совпадению в пределах почти такого же угла (173 мкрад) распространяется половина энергии.

Основной протокол измерения профиля пучка и расходимости

Проверка канала по картине Эйри

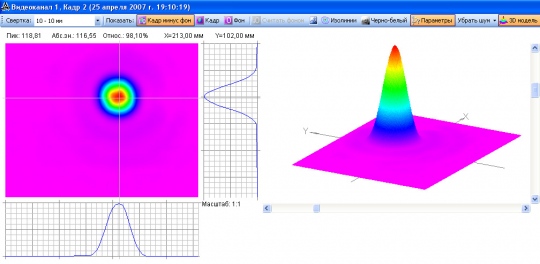
Обработка известного распределения, образуемого при дифракции плоской волны на круглой диафрагме, - так называемой картины Эйри, позволяет проверить правильность работы канала Регистратора РИЦ822. Диаметр первого темного кольца D может быть измерен оператором вручную с помощью курсора. Тем самым производится калибровка распределения, поскольку все измеряемые параметры фокального пятна в данном случае связаны с этим диаметром вполне определенными соотношениями. Например, диаметр пятна по уровню 0,5 максимальной интенсивности равен 0,422∙D , а диаметр пятна по уровню 0,5 полной энергии равен 0,438∙D. Остается только проверить показания Регистратора.

Измерение параметров на частоте 1 кГц

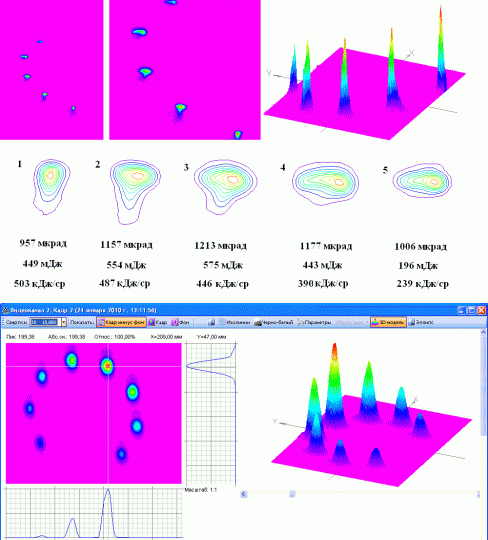
Интересный материал получен при регистрации пачки из 5-ти импульсов, следующих с частотой 1 кГц (их развертка на экране во времени по часовой стрелке осуществлена азимутальным дефлектором, вращающимся со скоростью 100 оборотов в секунду). Вверху слева приведено исходное зарегистрированное изображение (в масштабе 1:1), в центре изображение в масштабе 2:1 и справа соответствующее 3D-изображение. Видно, что пиковая интенсивность излучения в течение серии падает. Ниже приведены приведены распределения всех пяти импульсов в масштабе 8:1 и соответствующие результаты измерений расходимости по уровню 0,135 максимальной интенсивности. Приведены,также, значения энергии каждого импульса (измеренные параллельно работающим каналом измерения энергии). И, наконец, значения максимальной интенсивности, вычисленные по распределениям с использованием значений энергии. Расходимость и энергия возрастают в середине серии и падают в конце, но совместное действие этих двух факторов приводит к систематическому уменьшению максимальной интенсивности в течение серии.

Нижний рисунок иллюстрирует  изменение эффектиности накачки из-за плохой термостабилизации диодной матрицы (при частоте импульсов 1 кГц температура быстро нарастает  и проходит оптимальное значение, при котором эффективность накачки максимальна).

Влияние атмосферы на лазерный пучок

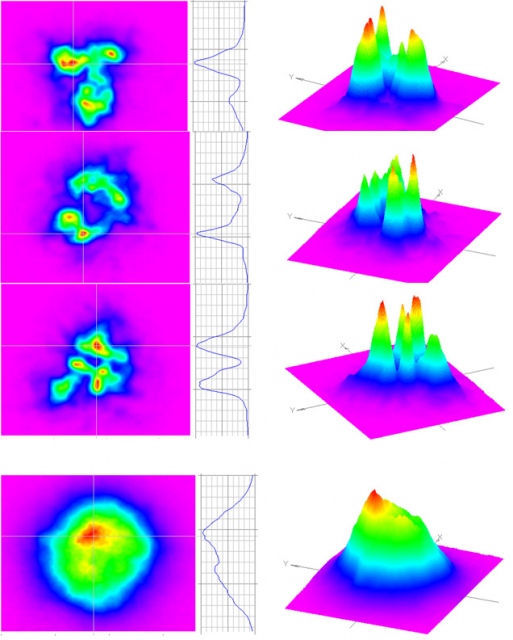
Рисунок иллюстрирует влияние турбулентной атмосферы на распределение интенсивности по сечению пучка при прохождении 500 метровой трассы. В данном случае, приведены 3 примера мгновенных распределений (из 75 зарегистрированных) и, внизу, распределение, усредненное по всем 75 кадрам. Несмотря на то, что в каждый момент времени пучок как бы «рассыпан» на несколько локальных областей, в среднем он остается достаточно компактным. ПО регистратора РИЦ822 позволяет оценить все параметры направленности для каждого кадра и для среднего распределения.

Измерение физической и геометрической расходимости лазерного пучка во времени.

Измерение расходимости излучения методом фокального пятна, т.е. по размеру диаметра пучка, определяемому в соответствии со стандартом ГОСТ Р ИСО 11146-1-2008 в фокальной плоскости собирающей линзы, дает представление только о полной расходимости.
Но в расходимости, в общем случае, имеются две основные компоненты:

- физическая θ_Ф, обусловленная дифракцией, наличием многих мод и неоднородностями в активной среде;

- геометрическая θ_Г, обусловленная кривизной волнового фронта на выходной апертуре лазера.

Полная расходимость θ_П является сверткой обеих составляющих.

Качество пучка (его фокусируемость) определяется только физической расходимостью. Геометрическая расходимость, не влияя на качество пучка, в ряде применений (например, при оптической локации) должна тщательно контролироваться с целью достижения требуемой полной расходимости.

Для раздельного измерения составляющих расходимости необходимо определить гиперболическую зависимость диаметра пучка в области перетяжки, формируемой при его фокусировке линзой или зеркалом (также, как при определении качества пучка согласно ГОСТ Р ИСО 11146-1-2008 ). На рисунке  приведены два варианта фокусировки пучка с плоским и выпуклым волновым фронтом на выходной апертуре лазера. Там же приведены обозначения величин, требующихся для дальнейшего изложения.

При отсутствии геометрической расходимости (при плоском фронте на выходе лазера) и при не слишком большом расстоянием L до линзы, на линзу поступает плоский волновой фронт и плоскость перетяжки практически совпадает с фокальной плоскостью линзы. Полная расходимость равна физической и определяется делением диаметра d_ф на фокусное расстояние линзы F.

При наличии геометрической расходимости на линзу поступает выпуклый (в данном примере) волновой фронт и плоскость перетяжки удаляется до положения Z₀. Тогда полная расходимость θ_П определяется делением диаметра d_П на фокусное расстояние линзы F, а физическая расходимость θ_Ф определяется, в первом приближении, делением диаметра перетяжки d_Ф* на ее удаление Z₀ от линзы.

Геометрическая расходимость θ_Г , в первом приближении, определяется по формуле:

где λ – длина волны лазерного излучения.

Однако численная оценка для реального варианта схемы измерений параметров волоконного лазера ( например, λ=1,07 мкм, d_А=10мм, L=10м) дает значение R более 2 км, что делает пренебрежимо малой разницу между F и Z₀.

Приведенное определение зависимости диаметра пучка в области перетяжки обычно производится сканированием пучка вдоль оси z с  помощью анализатора профиля. При этом предполагается что пучок и его параметры не изменяются во времени. Практика, однако, показывает, что для высокоэнергетических лазеров это не совсем так. Высокая лучевая нагрузка на оптические элементы в ряде случаев вызывает наведенные термодеформации и, как следствие, заметные изменения параметров пучка в течение пуска, которые также желательно контролировать.

При увеличении физической расходимости (например, за счет возрастания тепловых неоднородностей в активной среде) увеличивается диаметр перетяжки и гипербола в области перетяжки (зеленый цвет) смещается по вертикали вверх.

При изменении геометрической расходимости (например, за счет возникновения тепловой линзы на выходной оптике лазера) перетяжка Zo гиперболы смещается по горизонтали. При положительной тепловой линзе Zo* приближается к фокальной плоскости F (красный цвет), а при отрицательной  тепловой линзе Zo* удаляется от фокальной плоскости F (синий цвет).  Фокусное расстояние тепловой линзы определяется по формуле:

где: Z₀-положение перетяжки в начале пуска;

Z₀*-положение перетяжки в конце пуска;

L= -расстояние от выходной апертуры лазера до собирающей линзы.

В данном случае на каждом экране создается по два профиля пучка, соответствующих различным сечениям основного пучка, как показано на рисунке

Каждый профиль обрабатывается с помощью ПО Регистратора РИЦ822 по отдельности.
Параллельная регистрация профиля пучка в четырех плоскостях позволяет оценить не только изменение обеих составляющих расходимости, но и изменение во времени качества пучка, определяемого параметрами М2 и ВРР. Причем как для непрерывного режима работы, так и для импульсно-периодического.
Очевидно, что фокусные расстояния тепловых линз, определяемых по вышеприведенным формулам, очень велики и поэтому неудобны для построения их временных зависимостей FT(t) (все начинаются с бесконечности). Гораздо наглядней в этом смысле выглядят временные зависимости соответствующей оптической силы D(t)=1/ FT(t) тепловых линз, позволяющие оценивать, кроме того, и скорость нарастания оптической силы на различных временных отрезках генерации. По нашему опыту удобней всего оценивать оптическую силу тепловых линз в обратных километрах (км-1).
В качестве иллюстрации приведенной методики измерений на рисунке приведена одна из реализаций изменения оптической силы положительной тепловой линзы, возникающей на выходной оптике одномодового волоконного лазера мощностью 1.7 кВт.